1. 复习:关于 Rotation Matrix
- 三个用法
- 描述一个 frame 相对于另一个 frame 的姿态
- 将 point 由某一个 frame 的表达转换到另一个 frame(仅有相对转动变化)来表达
- 将 point(vector) 在同一个 frame 中进行转动
- 思考——空间中的 Rotation 是 3DOFs,那要如何把一般 rotation matrix 所表达的姿态,拆解成 3 次旋转角度,以应对到 3 个DOFs?
- 注意事项:
- Rotation 前后顺序需要明确定义(与移动不同,先向 X 移动后向 Y 移动与先向 Y 移动后向 X 移动可以互换顺序,而旋转不可以)
- 旋转转轴也需要明确定义。一般有两种「固定不动」旋转轴和「Body frame(随动)」转轴
- 两个拆解方式:
- 对方向**「固定不动」**的旋转轴旋转:Fixed angles …
- 对**「转动的 frame 当下所在」**的旋转方向旋转:Euler angles …
2. Fixed Angles
2.1 X-Y-Z Fixed Angles
由 angles 推算旋转矩阵 R(三次旋转分别针对 X,Y,Z 轴来做,X,Y,Z 轴是固定不动的,如下图蓝色坐标系)(逆时针为正)
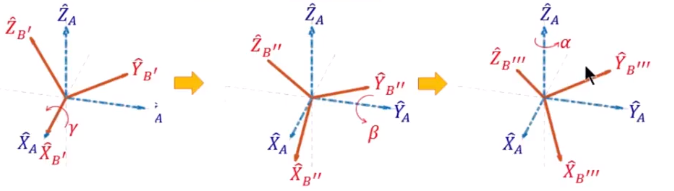
从左到右:绕X_A旋转,绕Y_A旋转,绕Z_A旋转
如何由三个角度推算出 Rotation Matrix?
$$
\begin{aligned}
\prescript{A}{B}{R}_{XYZ}(\gamma, \beta, \alpha) &= R_{Z}(\alpha)R_{Y}(\beta)R_{X}(\gamma)
\hspace{14em}
\textcolor{green}{v^{'} = \prescript{A}{B}{Rv} = R_{3}R_{2}R{_1}v}
\\
&= \begin{bmatrix}
c\alpha & -s\alpha & 0 \\
s\alpha & c\alpha & 0 \\
0 & 0 & 1 \\
\end{bmatrix}
\begin{bmatrix}
c\beta & 0 & s\beta \\
0 & 1 & 0 \\
-s\beta & 0 & c\beta \\
\end{bmatrix}
\begin{bmatrix}
1 & 0 & 0 \\
0 & c\gamma & -s\gamma \\
0 & s\gamma & c\gamma \\
\end{bmatrix}
\hspace{2em}
\textcolor{green}{先转的放「后面」:以operator来想,对某一个向量,}
\\
&= \begin{bmatrix}
c\alpha c\beta & c\alpha s\beta s\gamma - s\alpha c\gamma & c\alpha s\beta c\gamma + s\alpha s\gamma \\
s\alpha c\beta & s\alpha s\beta s\gamma + c\alpha c\gamma & s\alpha s\beta c\gamma - c\alpha s\gamma \\
-s\beta & c\beta s\gamma & c\beta c\gamma
\end{bmatrix}
\hspace{4em}
\textcolor{green}{「以同一个坐标为基准」,进行转动或移动的操作}
\end{aligned}
$$
EX1:

可以发现,更换转动顺序后,旋转矩阵数值与frame姿态都不相同,即是转动角度相同,顺序不同,最后的状态不同。

2.2 X-Y-Z Fixed Angles——由 R 推算 angles
$$ \prescript{A}{B}{R}_{XYZ}(\gamma, \beta, \alpha) = \begin{bmatrix} c\alpha c\beta & c\alpha s\beta s\gamma - s\alpha c\gamma & c\alpha s\beta c\gamma + s\alpha s\gamma \ s\alpha c\beta & s\alpha s\beta s\gamma + c\alpha c\gamma & s\alpha s\beta c\gamma - c\alpha s\gamma \ -s\beta & c\beta s\gamma & c\beta c\gamma \end{bmatrix}
\begin{bmatrix} r_{11} & r_{12} & r_{13} \ r_{21} & r_{22} & r_{23} \ r_{31} & r_{32} & r_{33} \ \end{bmatrix} $$
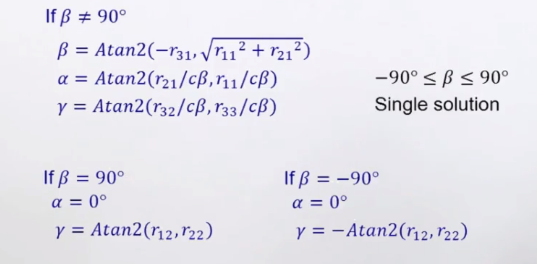
EX1:先给旋转矩阵内容,计算三个角度

先对X转60°,再对Y转30°,没有对Z转
3. Euler Angles
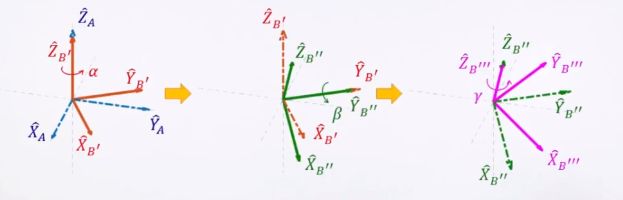
3.1 Z-Y-X Euler Angles-由 angles 推算 R (绕被转动转轴去做旋转)
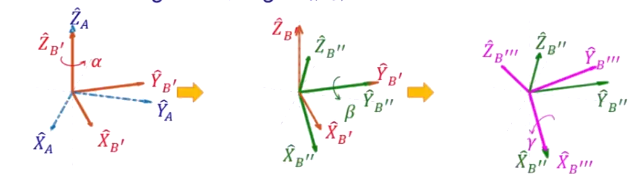
从左到右:先根据 Z_B转,在根据Y_B转,最后根据X_B转
如何由三个角度推出 Rotation Matrix?
$$ \prescript{A}{B}{R}_{z^{'}Y^{'}X^{'}}(\alpha, \beta, \gamma) = \prescript{A}{B^{'}}{R}\prescript{B^{'}}{B^{''}}{R}\prescript{B^{''}}{B}{R} = R_{Z^{'}}(\alpha)R_{Y^{'}(\beta)}R_{X^{'}}(\gamma) $$先转的放【前面】:以 mapping 来想,对某一个向量,从最后一个 frame【逐渐转动或移动】来回到第一个 frame:
$$ \textcolor{green}{^{A}P = ^{A}_{B}R^{B}P = R_{1}R_{2}R_{3}^{B}P} \\ \begin{aligned} &= \begin{bmatrix} c\alpha & -s\alpha & 0 \\ s\alpha & c\alpha & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} c\beta & 0 & s\beta \\ 0 & 1 & 0 \\ -s\beta & 0 & c\beta \\ \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & c\gamma & -s\gamma \\ 0 & s\gamma & c\gamma \\ \end{bmatrix} \\ &= R_{Z}(\alpha)R_{Y}(\beta)R_{X}(\gamma) = \prescript{A}{B}{R}_{XYZ}(\gamma, \beta, \alpha) \end{aligned} \\ \textcolor{green}{和X-Y-Z \hspace{0.4em} Fixed \hspace{0.4em} angle得到一样的R} $$欧拉angle与Fixed Angle具有简单对应
EX1:

EX2: Euler(Y30,X60) v.s. Fixed(X60,Y30)
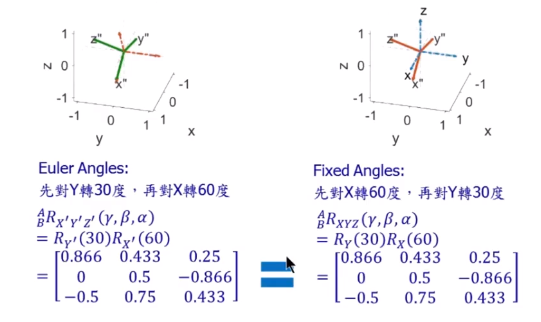
3.2 Z-Y-Z Euler Angles - 由 angles 推算 Rotation Matrix
旋转矩阵表达法:先转放前面,后转放后面(反向 mapping)
$$ \begin{aligned} \prescript{A}{B}{R}_{z^{'}Y^{'}X^{'}}(\alpha, \beta, \gamma) &= R_{Z^{'}}(\alpha)R_{Y^{'}(\beta)}R_{X^{'}}(\gamma) \\ \textcolor{green}{先转的放「前面」} \\ &= \begin{bmatrix} c\alpha c\beta c\gamma - s\alpha s\gamma & -c\alpha c\beta s\gamma - s\alpha c\gamma & c\alpha s\beta \\ s\alpha c\beta c\gamma + c\alpha s\gamma & -s\alpha c\beta s\gamma + c\alpha c\gamma & s\alpha s\beta \\ -s\beta c\gamma & s\beta s\gamma & c\beta \end{bmatrix} \end{aligned} $$
EX: Revisit Euler Angles-2 的范例

以此ZYZ旋转矩阵转出的状态和之前的状态一样
争取一个特定的 R,有多种的拆解组合:
- 12 种 Euler Angles 和 12 种 Fixed Angles;
- 存在 Duality —共 12 种对 Principal Axes 连 3 次转动的拆解方法;
4. Angle-Axis 表达法
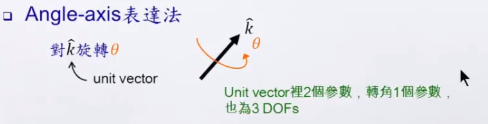
k是单位向量,vector有2个参量,再加上转角,也是3Dofs
5. Quaternion (四元数)表达法
$$ q \hspace{0.5em} = \hspace{0.5em} \epsilon_{4} + \epsilon_{1}\overline{l} + \epsilon_{2}\overline{j} + \epsilon_{3}\overline{k} \hspace{0.5em} = \hspace{0.5em} \cos \frac{\theta}{2} + \sin \frac{\theta}{2}(k_{x}\overline{l} + k_{y}\overline{j} + k_{z}\overline{k}) $$其中:
$$ \epsilon_{1}^{2} + \epsilon_{2}^{2} + \epsilon_{3}^{2} + \epsilon_{4}^{2} = 1 $$这里,四个参数加一个条件约束,也为 3DOFs。